Greedy Algorithms Explained: A Beginner’s Guide with Examples

Learn how greedy algorithms work and when to use them, and see real-world examples with simple explanations.

🤑 What is Greedy in Algorithms?

The word “Greedy” itself gives the meaning.
It means picking the best option right now, without thinking about the future.

In real life, imagine you are hungry at a buffet. You see pizza and salad. A greedy choice would be to grab the pizza immediately because it looks best at that moment, without thinking if something tastier might come later.

In algorithms, the greedy method works the same way.
At each step, you choose what looks like the best immediate option.
By repeating this, you hope to reach the best overall solution.

Greedy means picking the best option at the moment, without worrying about what comes later.

---

🤔 Where Do We Use Greedy in Real Life?

Greedy is not something we use alone in theory , it shows up in real-world problems too.

• Greedy + Sorting → Imagine you have many meetings in a day. You want to attend the maximum number. If you sort meetings by finishing time and always pick the earliest one that fits, you’re using greedy.

• Greedy + Priority Queue (Heap) → When compressing files (like ZIP or MP3), greedy is used to always combine the smallest pieces first (this is how Huffman Coding works behind the scenes).

• Greedy + Graphs → When Google Maps finds the shortest path, it keeps moving to the nearest unvisited place at each step , that’s greedy in action.

• Greedy + Union-Find → When connecting different cities with minimum cost (like laying cables or building roads), greedy helps pick the cheapest connections step by step.

So, greedy is everywhere: from scheduling your day, to compressing data, to routing on maps, to building networks.

---

🪜 The Step-by-Step Greedy Approach

Greedy works in a very simple way. It follows these steps:

1. Look at the options you have right now.
   Don’t think about the whole future, just focus on the current step.

2. Pick the best option available at this moment.
   This is your greedy choice.

3. Add it to your solution.
   Update your answer with the choice you just made.

4. Move to the next step and repeat.
   Again, choose what looks best right now.

5. Stop when you reach the goal or no choices are left.

For example, imagine you have coins of ₹20, ₹10, and ₹5.
Your friend needs ₹35.

• Look at the options you have right now.
  You have coins of ₹20, ₹10, and ₹5. Your friend needs ₹35.

• Pick the best option available at this moment (Greedy choice).
  The biggest coin is ₹20 → pick it. Now you need ₹15 more.

• Add it to your solution.
  Solution so far = ₹20.

• Move to the next step and repeat.
  Next best coin is ₹10 → pick it. Now you need ₹5 more.

  Again repeat → pick ₹5. Now you need ₹0.

• Stop when you reach the goal or no choices are left.
  Total coins used = ₹20 + ₹10 + ₹5 = ₹35 ✅

But notice, there are other ways too:

You could also give seven ₹5 coins, or three ₹10 coins and one ₹5 coin.
But greedy says: “pick the easiest best option right now” → that’s why you chose 20, then 10, then 5.

You didn’t worry about whether the ₹20 coin might be useful later you just solved the problem right now.

---

🤘 Greedy Example with a Meta Level-1 Question

Here’s a real-world-style interview problem (actually asked in Meta’s online assessments):

A cafeteria has a row of N seats, numbered 1 to N.
Social distancing rules say:

• Each diner must keep at least K empty seats on the left and right.

• M Diners are already seated at positions S[i].

• No two diners are in the same seat, and the current seating follows the rules.

👉 The task: Find the maximum number of new diners that can still sit without breaking the rules.

Example

Let’s take:

• N = 10 (10 seats in total)

• K = 1 (1 empty seat required on both sides)

• M = 2 (2 diners already seated)

• S = [2, 6] (diners are sitting at seat 2 and seat 6)

The table looks like this

1 2 3 4 5 6 7 8 9 10
B X B - B X B - - -

• Seat 2 blocks seat 1 and 3.

• Seat 6 blocks seat 5 and 7.

Now the free seats are: 4, 8, 9, 10.

👉 If we seat people greedily (always taking the earliest available valid seat):

• Put one at seat 4 → blocks seat 4 and 5 (but 5 is already blocked).

• Put one at seat 8 → blocks 8 and 9.

• Finally, seat one at 10.

✅ Total = 3 additional diners can be seated.

Question Link in Meta site → Cafeteria Problem

Now, I’ll share the answer below. But without scrolling down, just try to decode the logic yourself first. Think about how greedy and sorting can be applied here.

Solution Approach

1. Look before the first diner

• First diner is at seat 2.

• Because of distancing, seat 1 is blocked.

• That means no space before diner 2.

👉 Left side gives 0 new diners.

2. Look between diners

• Between seat 2 and seat 6, the free seats are [3, 4, 5].

• But seat 3 (close to 2) and seat 5 (close to 6) are blocked.

• That leaves only seat 4.

Middle gap gives 1 new diner.

3. Look after the last diner

• Last diner is at seat 6.

• Free seats are [7, 8, 9, 10].

• Seat 7 is blocked because of distancing.

• Remaining free seats = [8, 9, 10].

• Now place diners one by one, skipping 1 seat each time:

  • Place at seat 8.

  • Skip seat 9.

  • Place at seat 10.

👉 Right side gives 2 new diners.

✅ Total

• Left side = 0

• Middle = 1

• Right side = 2

Answer = 3 new diners (at seats 4, 8, 10)

Simply:

1. Sort the existing diners – so we can look at the empty spaces between them in order.

2. Check the left side – from seat 1 to just before the first diner (excluding the blocked K seats).

3. Check the gaps between diners – for each pair of diners, calculate how many free seats exist between them after applying the distancing rule. Place as many new diners as possible inside that gap.

4. Check the right side – from just after the last diner (excluding the blocked K seats) to seat N.

5. Add them all up – the sum from left side + middle gaps + right side = the maximum number of additional diners.

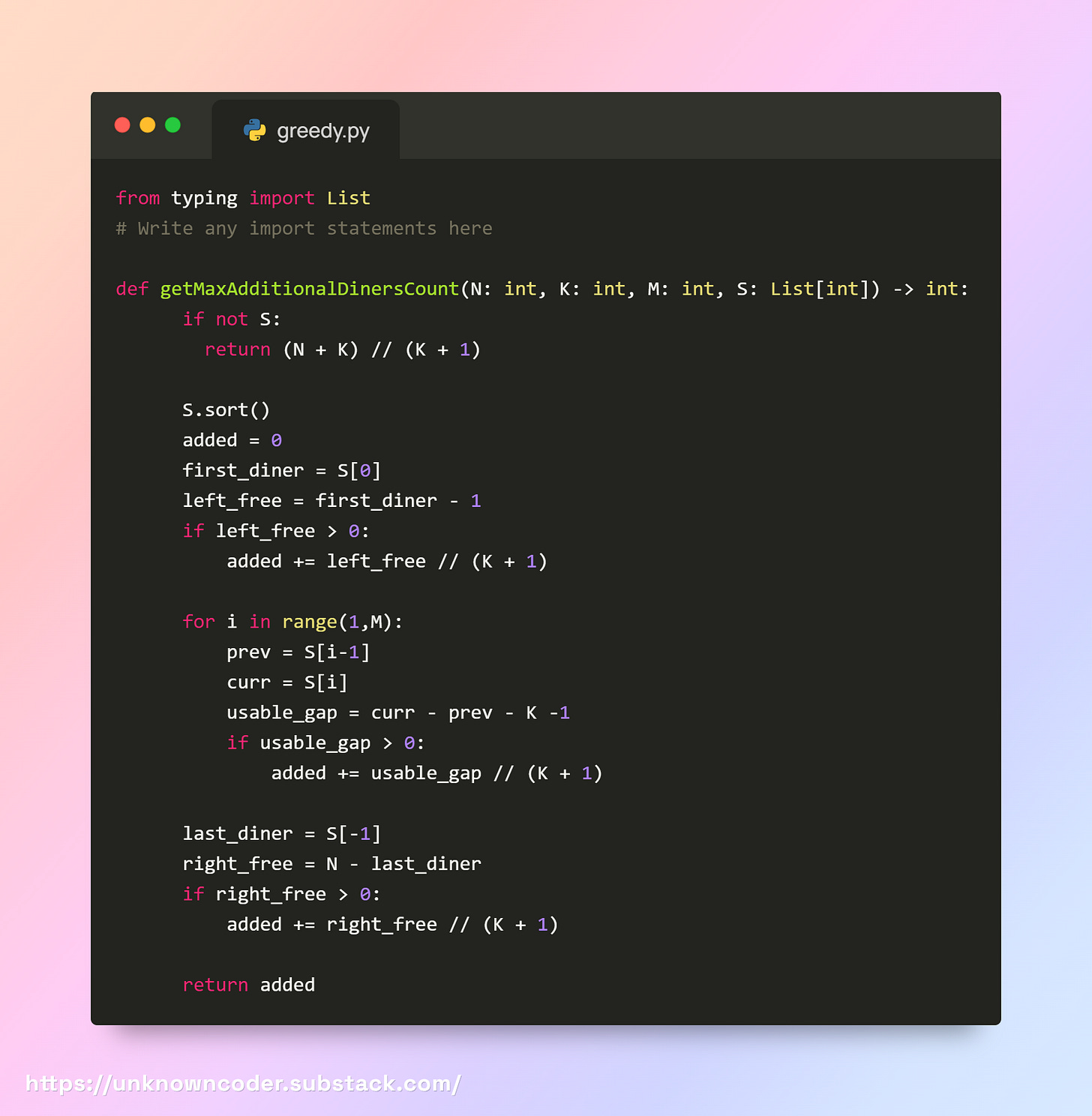
Code Solution

Let’s go step by step using your test case:

• Input:

N = 10  # total seats
K = 1   # need 1 empty seat between diners
M = 2   # 2 diners already seated
S = [2, 6]  # diners at seats 2 and 6

Step 1: Check if S is empty

if not S:
    return (N + K) // (K + 1)

• S is not empty ([2, 6]), so we skip this.

Step 2: Sort S

S.sort()

• Already sorted: [2, 6].

Step 3: Initialize added diners

added = 0

• added = 0

Step 4: Check seats to the left of the first diner

first_diner = S[0]   # 2
left_free = first_diner - 1  # 2 - 1 = 1
if left_free > 0:
    added += left_free // (K + 1)  # 1 // 2 = 0

• Seats before seat 2: only seat 1.

• Cannot place a diner because K=1 requires at least 2 seats (1 for diner + 1 empty).

• added = 0

Step 5: Check gaps between diners

for i in range(1, M):  # i = 1
    prev = S[i-1]  # 2
    curr = S[i]    # 6
    usable_gap = curr - prev - K - 1  # 6 - 2 - 1 - 1 = 2
    if usable_gap > 0:
        added += usable_gap // (K + 1)  # 2 // 2 = 1

• Seats between 2 and 6: [3, 4, 5].

• K=1, so we must leave 1 seat next to each existing diner.

• Usable seats = 2 ([4,5] can only fit 1 diner).

• Place 1 new diner here.

• added = 1

Step 6: Check seats to the right of the last diner

last_diner = S[-1]  # 6
right_free = N - last_diner  # 10 - 6 = 4
if right_free > 0:
    added += right_free // (K + 1)  # 4 // 2 = 2

• Seats after seat 6: [7, 8, 9, 10].

• Place diners at seats 8 and 10 (keeping 1 seat apart).

• added = 1 + 2 = 3

Step 7: Return result

return added  # 3

Here's how Greedy works here

• Fill from left to right in each free segment – always place diners as early as possible without breaking the K-seat rule.

• Maximize each gap – calculate how many diners fit in a gap using usable_gap // (K + 1).

• Handle all segments separately – check the left edge, gaps between diners, and right edge to get the total maximum.

If you want to practice similar problems, give this one a try

• Maximize Distance to Closest Person (LeetCode 849)

• Non-overlapping Intervals (LeetCode 435)

• Meeting Rooms II (LeetCode 253)

• Minimum Number of Arrows to Burst Balloons (LeetCode 452)

• Maximum Number of Events That Can Be Attended (LeetCode 1353)

---

How to Spot a Greedy Problem

1. Local choice works globally – Best immediate choice leads to overall best solution.

2. Sortable elements – Decisions can be made after sorting numbers, intervals, or positions.

3. Independent segments – Parts of the problem can be handled separately without affecting others.

---

When You Can’t Use Greedy

1. No Greedy Choice Property

   • Local optimum does not lead to the global optimum.

   • Example: Coin change problem with coins [1, 3, 4] and target 6. Choosing the largest coin first (greedy) gives 4 + 1 + 1 = 3 coins, but the optimal is 3 + 3 = 2 coins.

2. Dependent Subproblems

   • Decisions in one part affect the solution in another.

   • Example: Some DP problems like 0/1 Knapsack, where choosing an item now may prevent a better combination later.

3. Requires Lookahead

   • When you need to consider future consequences before making a choice.

   • Example: Some scheduling problems with complex constraints, or certain graph problems like shortest path with negative weights (requires Bellman-Ford, not greedy Dijkstra).

---

Greedy is one of the most widely used techniques in problem-solving around the world. By understanding its patterns and practicing problems like these, you can quickly improve your algorithmic thinking. Hope you learned something new today! Subscribe for more content like this and keep learning.

---