Day 8 : Mastering 7 Sorting Algorithms
Unpacking Classic Sorting Approaches Every Developer Must Know
Instead of relying only on built-in sorting functions, itâs important to understand how sorting actually works under the hood. Almost every programming language provides a default sorting method where you can simply call a function and get your list ordered. But what if, during an interview, someone asks: âCan you explain the sorting approach that Python (or any language) uses?â
Thatâs where mastering the fundamental sorting algorithms comes in. By learning them, youâll not only be able to answer such questions with confidence, but youâll also sharpen your problem-solving skills and develop an intuition for algorithm efficiency.
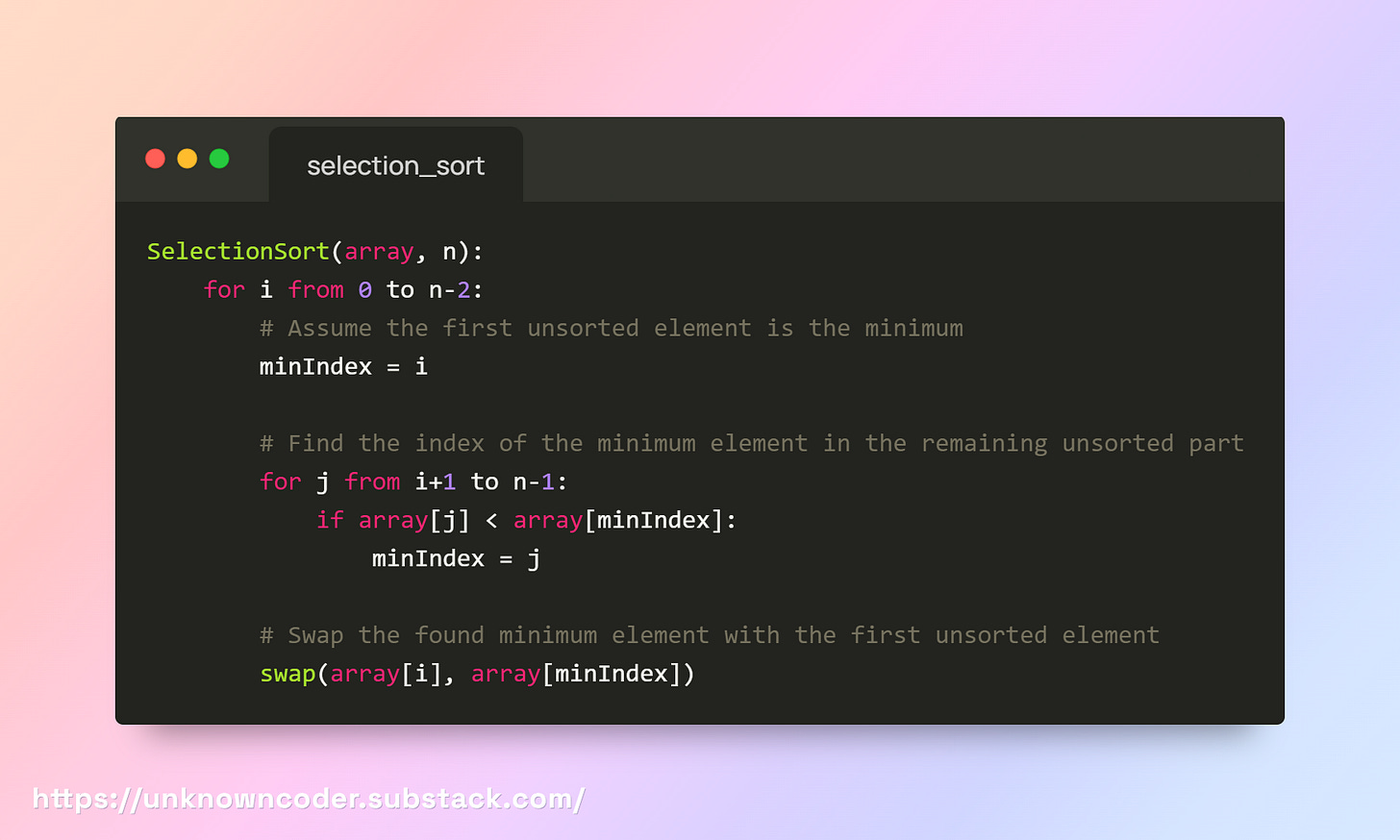
1. Selection Sort
Selection Sort works by repeatedly finding the minimum element from the unsorted portion of the array and placing it at the beginning.
It divides the array into two parts:
Sorted part (at the front)
Unsorted part (remaining elements)
At each step, it picks the smallest element from the unsorted part and swaps it with the first unsorted element.
Letâs take the array:
a = [5, 2, 6, 3, 1]Step 1: Start at index 0
Look at the whole array
[5, 2, 6, 3, 1].Minimum element =
1(at index 4).Swap
a[0]witha[4].
a = [1, 2, 6, 3, 5]
Step 2: Move to index 1
Now consider the unsorted part
[2, 6, 3, 5].Minimum element =
2(already at index 1).No swap needed.
a = [1, 2, 6, 3, 5]Step 3: Move to index 2
Now consider
[6, 3, 5].Minimum element =
3(at index 3).Swap
a[2]witha[3].
a = [1, 2, 3, 6, 5]Step 4: Move to index 3
Now consider
[6, 5].Minimum element =
5(at index 4).Swap
a[3]witha[4].
a = [1, 2, 3, 5, 6]Step 5: Last element
Only one element left (
6), itâs already sorted.
Final Sorted Array:
a = [1, 2, 3, 5, 6]Imagine youâre organizing a stack of books on a shelf in ascending order based on their height. You start by finding the shortest book and placing it at the leftmost position. Then, you move on to the remaining books, finding the next shortest one and placing it next to the first book. This process continues until all the books are arranged in order of increasing height.
Time Complexity
Best Case: O(n²)
Average Case: O(n²)
Worst Case: O(n²)
Space Complexity
O(1)
LeetCode problems to practice
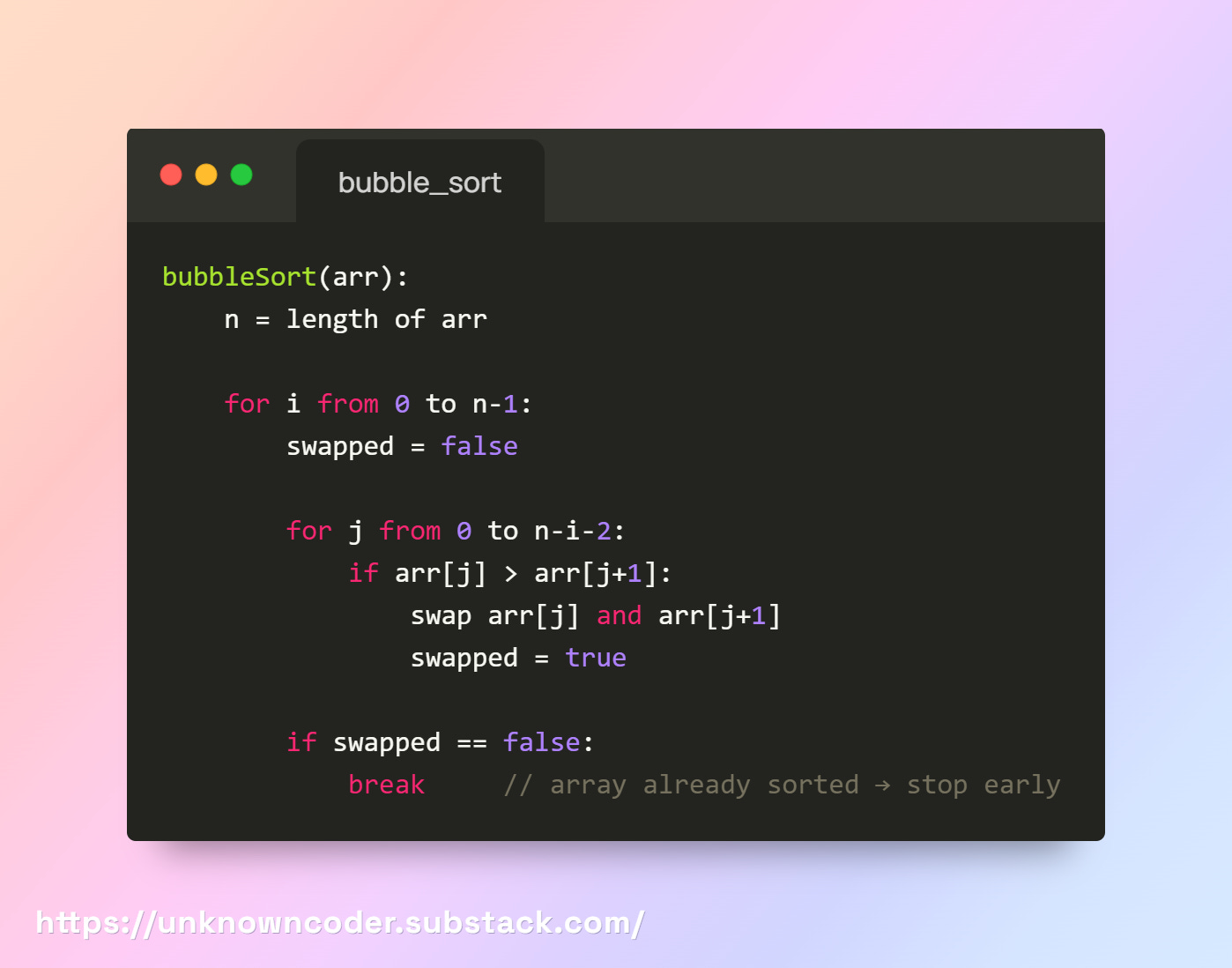
2. Bubble Sort
Bubble Sort repeatedly steps through the array, compares each pair of adjacent elements and swaps them if they are in the wrong order. After each full pass through the array, the largest element among the unsorted portion âbubblesâ to its correct place at the end. It divides the array into:
Sorted part (at the end)
Unsorted part (at the front)
Itâs an in-place, stable algorithm. With a small optimisation (stop if no swaps in a pass), it becomes adaptive (best case linear).
Example:
a = [5, 2, 6, 3, 1]Pass 1 (compare adjacent pairs leftâright):
Compare 5 & 2 â swap â [2, 5, 6, 3, 1]
Compare 5 & 6 â no swap â [2, 5, 6, 3, 1]
Compare 6 & 3 â swap â [2, 5, 3, 6, 1]
Compare 6 & 1 â swap â [2, 5, 3, 1, 6]
After pass 1: largest element 6 is in final position (end).
Pass 2 (ignore the last sorted element):
Compare 2 & 5 â no swap â [2, 5, 3, 1, 6]
Compare 5 & 3 â swap â [2, 3, 5, 1, 6]
Compare 5 & 1 â swap â [2, 3, 1, 5, 6]
After pass 2: second-largest (5) now just before the last.
Pass 3:
Compare 2 & 3 â no swap â [2, 3, 1, 5, 6]
Compare 3 & 1 â swap â [2, 1, 3, 5, 6]
After pass 3: array getting closer.
Pass 4:
Compare 2 & 1 â swap â [1, 2, 3, 5, 6]
Now sorted.
Tip: if a full pass makes zero swaps, you can stop early, thatâs how Bubble Sort achieves a best case of O(n) on an already-sorted array.
Imagine repeatedly scanning a line of people and asking each adjacent pair to swap if the shorter person is behind the taller one, tall people gradually move (âbubbleâ) to the back of the line.
Pseudocode
Time Complexity
Best Case: O(n) â if optimized with an early-exit check (already sorted).
Average Case: O(n²)
Worst Case: O(n²)
Space Complexity
O(1) (in-place)
LeetCode problems to practice
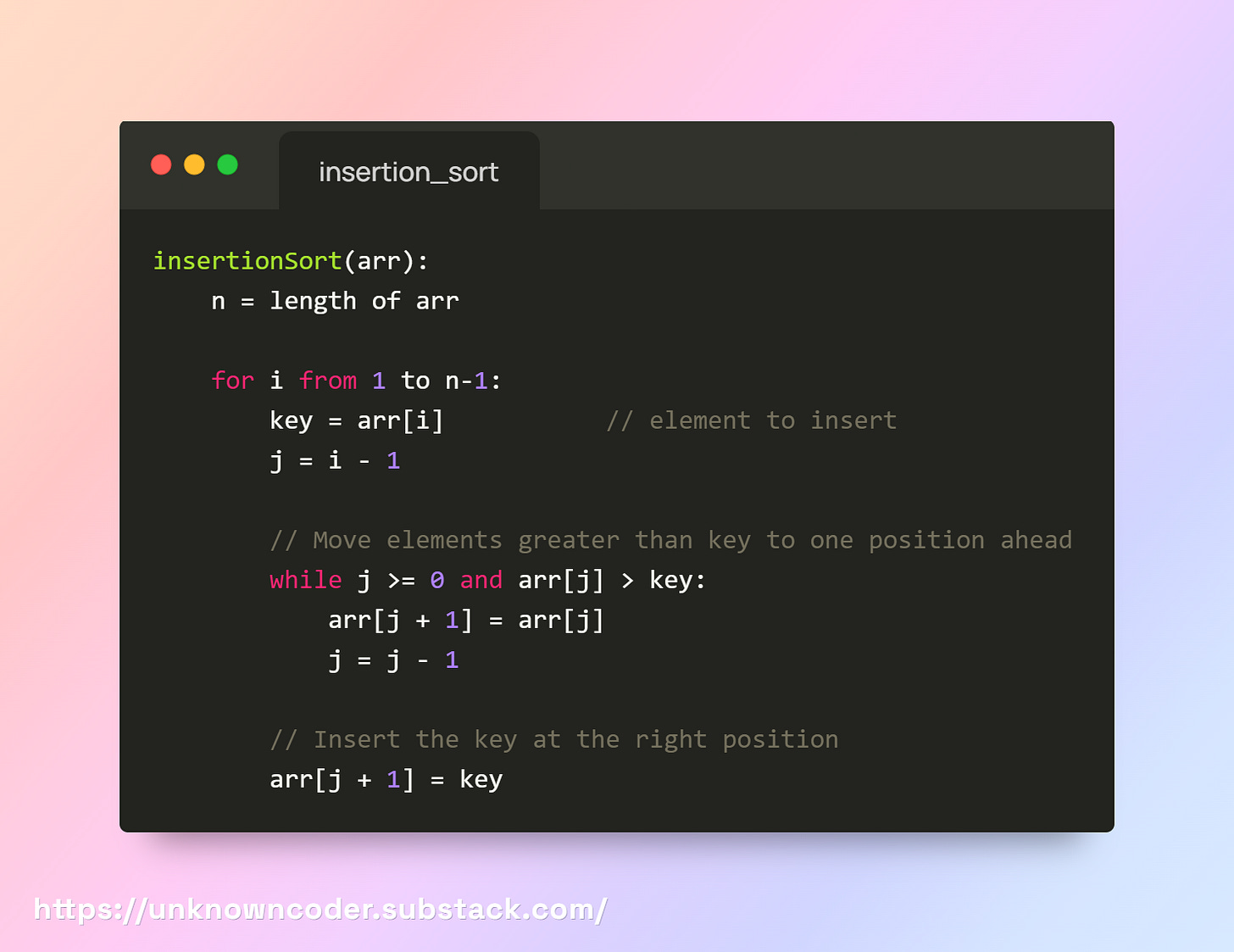
Insertion Sort
Insertion Sort builds the final sorted array one element at a time. It takes the next element from the unsorted portion and inserts it into the correct position in the sorted part by shifting larger elements to the right. It is in-place and stable, and itâs adaptive (very fast for nearly-sorted data). Commonly used for small arrays or as the base case inside more advanced sorts.
Maintain a sorted subarray a[0..i-1].
Take element a[i], compare it backwards with the sorted subarray, shift elements right until you find the correct spot, and insert a[i].
Example:
a = [5, 2, 6, 3, 1]Step 1: i = 1 (value = 2)
Compare 2 with 5 â shift 5 right â insert 2 at index 0
a = [2, 5, 6, 3, 1]
Step 2: i = 2 (value = 6)
Compare 6 with 5 â 6 ⼠5 â no shifts â insert 6 at index 2
a = [2, 5, 6, 3, 1]
Step 3: i = 3 (value = 3)
Compare 3 with 6 â shift 6 â [2, 5, 6, 6, 1]
Compare 3 with 5 â shift 5 â [2, 5, 5, 6, 1]
Compare 3 with 2 â 2 ⤠3 â stop and insert 3 at index 1
a = [2, 3, 5, 6, 1]
Step 4: i = 4 (value = 1)
Compare 1 with 6 â shift 6 â [2, 3, 5, 6, 6]
Compare 1 with 5 â shift 5 â [2, 3, 5, 5, 6]
Compare 1 with 3 â shift 3 â [2, 3, 3, 5, 6]
Compare 1 with 2 â shift 2 â [2, 2, 3, 5, 6]
Insert 1 at index 0 â [1, 2, 3, 5, 6]
Final Sorted Array: a = [1, 2, 3, 5, 6]
Think of sorting a hand of playing cards: you take one card at a time from the deck and insert it into the correct position in your already-sorted hand by sliding larger cards to the right.
Time Complexity
Best Case: O(n) â when the array is already (or nearly) sorted (only one comparison per element).
Average Case: O(n²)
Worst Case: O(n²)
Space Complexity
O(1) (in-place)
LeetCode problems to practice
As you can see, all these basic sorting algorithms, Selection Sort, Bubble Sort, and Insertion Sort have a worst-case time complexity of O(N²).
While theyâre great for understanding the core concepts of sorting, in real-world applications we rarely rely on them due to their inefficiency with large datasets.
In the next part, weâll explore how to sort an array in O(N) time and understand the logic behind those faster approaches.