Day 3 (Part 2): Sliding Window – Mastering Variable Length Patterns

Learn the core idea of non-fixed window and how it powers real interview problems.

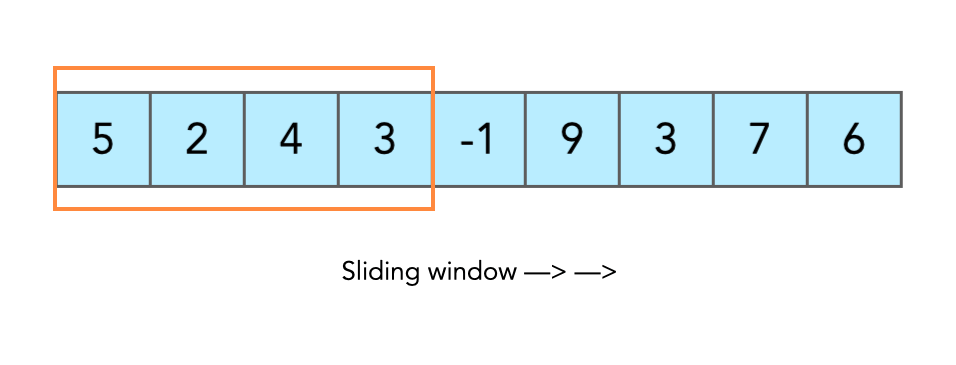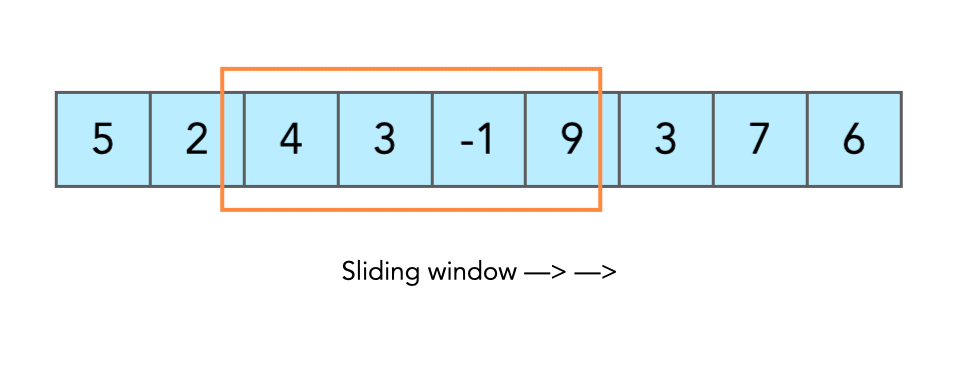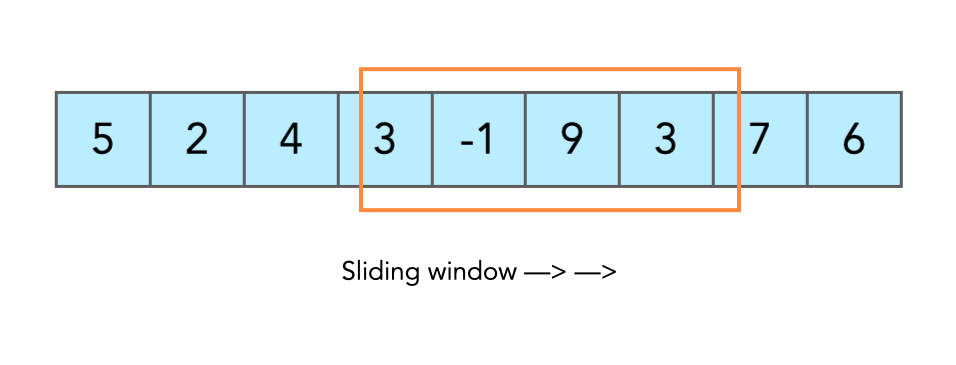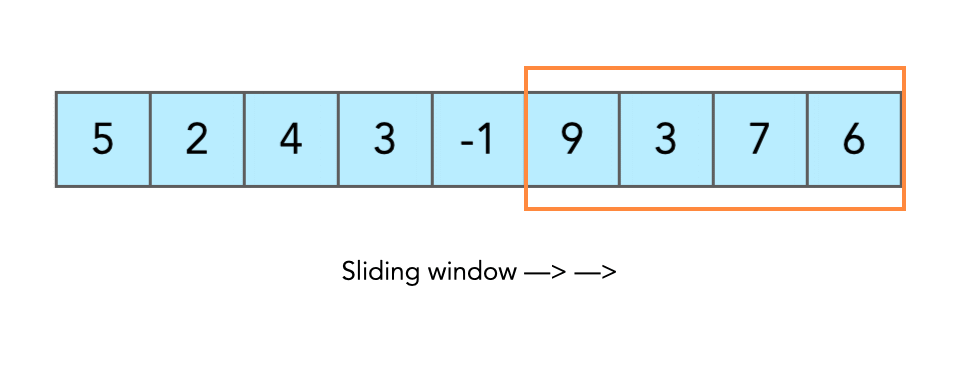
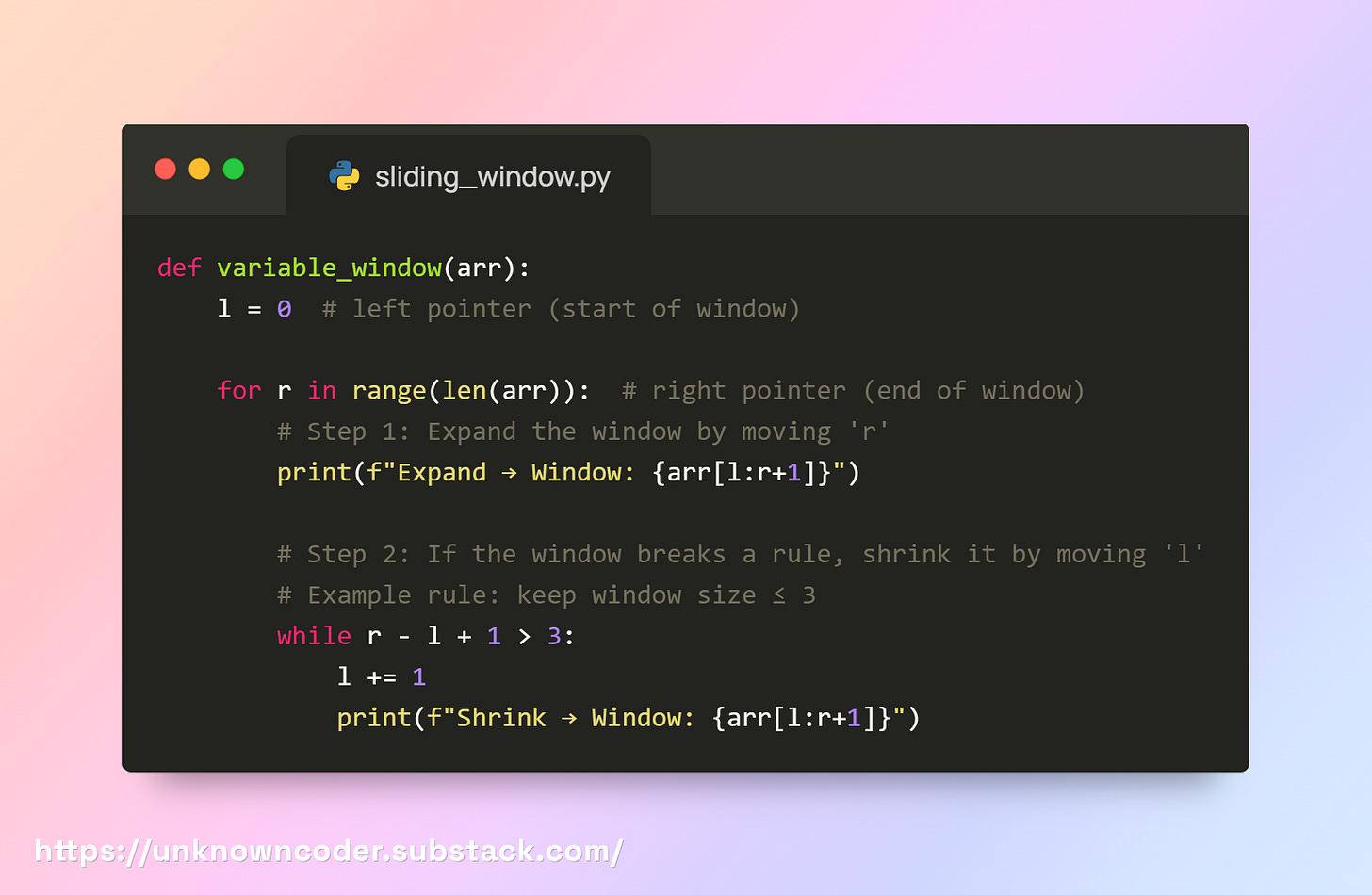
We’ve already seen what a sliding window is and the fixed window type. In the fixed window, we had two pointers l and r moving together, if l increases, r also increases. But now in a non-fixed (variable) window, we still have the same two pointers, only this time there’s no strict rule. We can shrink or expand the window based on the problem. This flexibility is what makes variable window powerful and a must-know for cracking tough interview questions.

Working with Variable Sliding Window

Here is how the technique works:

Input: [1, 2, 3, 4, 5]

Output:

Expand → Window: [1]
Expand → Window: [1, 2]
Expand → Window: [1, 2, 3]
Expand → Window: [1, 2, 3, 4] # window exceed len <= 3
Shrink → Window: [2, 3, 4] # moving l to +1
Expand → Window: [2, 3, 4, 5]
Shrink → Window: [3, 4, 5]

Explanation

• We use two pointers: l (left) and r (right).

• The right pointer (r) always moves forward to expand the window.

• If some condition breaks (like size > 3, sum > K, duplicate found, etc.), we move the left pointer (l) forward to shrink the window.

• This “expand + shrink” flexibility is what makes the variable sliding window powerful.

Think of it like a rubber band: r stretches it, l loosens it when needed.

---

Let’s dive into the real problem

Amazon’s Favourite Question (Fruit Collector) Leetcode 904

You are walking along a row of fruit trees.

• Each tree produces exactly one type of fruit.

• The trees are arranged in a line, represented by an array of integers where each integer is a fruit type.

• You have two baskets, and each basket can only hold one type of fruit.

Starting at any tree, you want to collect as many fruits as possible by moving only to the right.
You must stop collecting once you encounter a third fruit type (because you only have two baskets).

Return the maximum number of fruits you can collect in a single trip.

Example 1

Input:

trees = [1, 2, 1]

Output:

3

You can collect all: [1, 2, 1].

Example 2

Input:

trees = [0, 1, 2, 2]

Output:

3

You can collect [1, 2, 2].

Example 3

Input:

trees = [1, 2, 3, 2, 2]

Output:

4

You can collect [2, 3, 2, 2].

---

Your Turn Before Seeing the Solution

Before you look at the solution, try to solve it yourself.

Challenge yourself and see if you can find the answer in your own way.

---

Solution

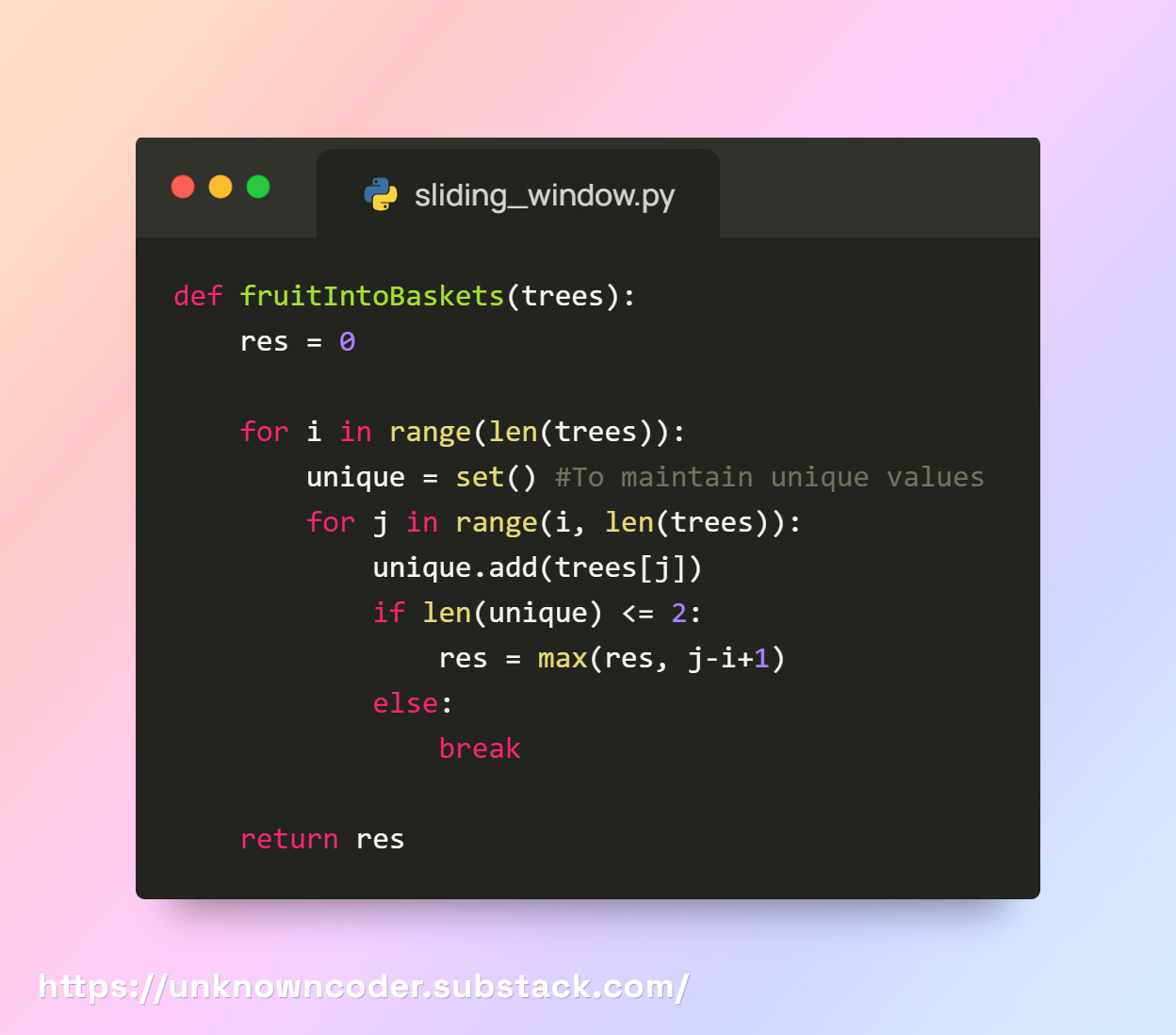
Let’s Start with the Brute Force Approach

The problem is, we have only two baskets, but the trees may have many types of fruits.
We need the longest sequence of trees where we can collect fruits into just 2 baskets.

Example: tree = [1, 2, 3, 2, 2, 3]

👉 Start from the first element (1):

• Take [1] → basket = {1} ✅ (1 type only)

• Take [1,2] → basket = {1,2} ✅ (2 types allowed)

• Take [1,2,3] → basket = {1,2,3} ❌ (3 types, not allowed)
  So max length from index 0 = 2 (and here we know that there are more than 3 tree types, so move on to the next element).

👉 Now start from the second element (2):

• Take [2] → basket = {2} ✅

• Take [2,3] → basket = {2,3} ✅

• Take [2,3,2] → basket = {2,3} ✅

• Take [2,3,2,2] → basket = {2,3} ✅

• Take [2,3,2,2,3] → basket = {2,3} ✅
  So max length from index 1 = 5

👉 Start from the third element (3):

• Take [3] → basket = {3} ✅

• Take [3,2] → basket = {3,2} ✅

• Take [3,2,2] → basket = {3,2} ✅

• Take [3,2,2,3] → basket = {3,2} ✅
  So max length from index 2 = 4

👉 Start from the fourth element (2):

• Take [2] → basket = {2} ✅

• Take [2,2] → basket = {2} ✅

• Take [2,2,3] → basket = {2,3} ✅
  So max length from index 3 = 3

👉 Start from the fifth element (2):

• Take [2] → basket = {2} ✅

• Take [2,3] → basket = {2,3} ✅
  So max length from index 4 = 2

👉 Start from the sixth element (3):

• Take [3] → basket = {3} ✅
  So max length from index 5 = 1

✅ Final Answer = maximum of all = 5

Here's what the code looks like

Complexity

• Outer loop = O(n)

• Inner loop = O(n)

• Each set operation = O(1) (average)

• Total: O(n²) time, O(1) extra space

This brute force solution works fine when the array is small.
But if the interviewer is from Amazon/Meta/etc., they won’t stop here.
They’ll usually say something like:

“Okay, this is correct… But can you make it faster? Right now you’re checking every starting point and going one by one, can you find a way to reuse your work instead of restarting each time?”

That’s their hint to push you toward the sliding window approach, which reduces the time from O(n²) to O(n).

---

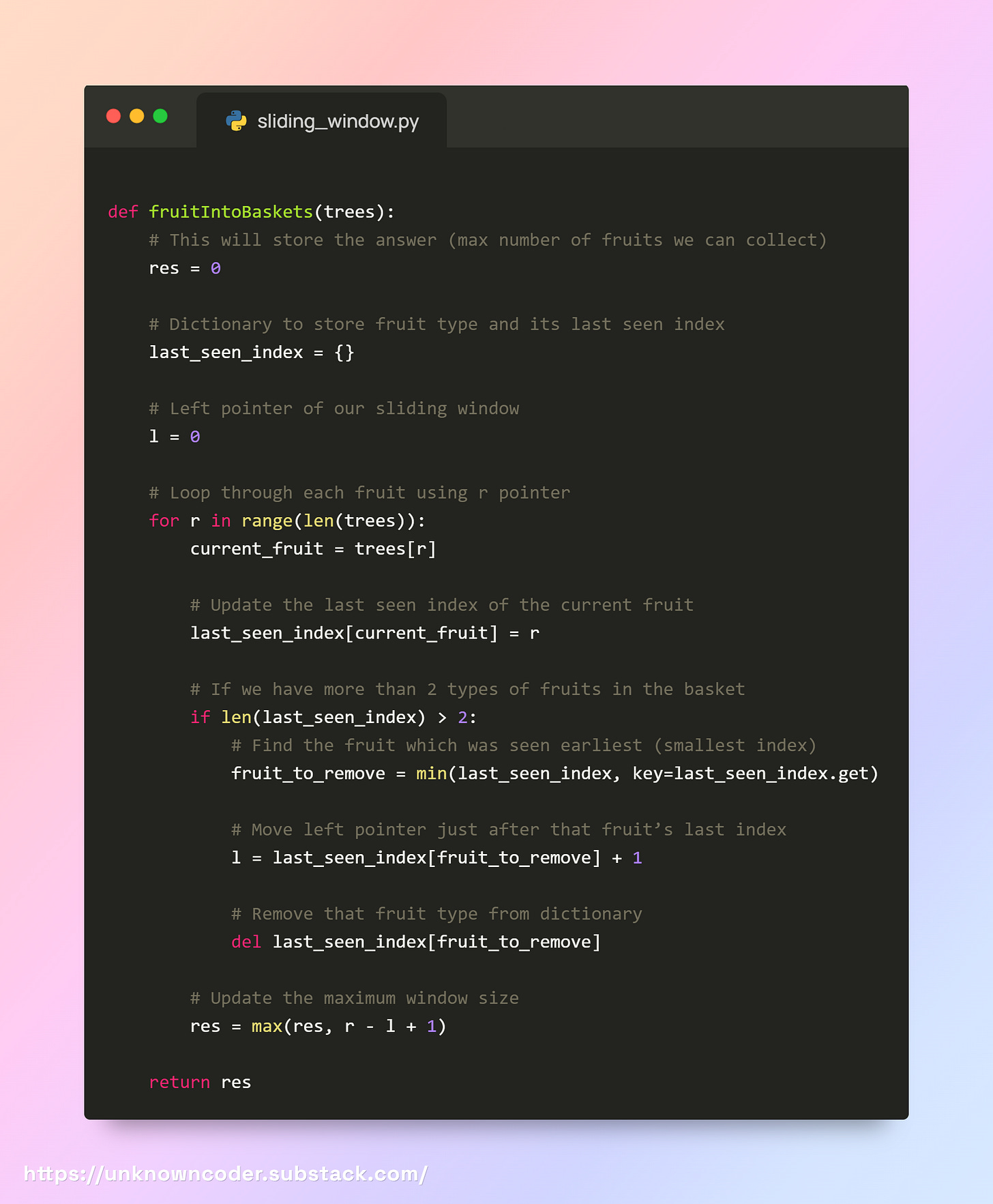
Optimal Approach Using sliding window

Now we are going to use a variable-length sliding window.
That means we have two pointers:

• l → left pointer (start of the window)

• r → right pointer (end of the window)

Step 1:

At the beginning, both l and r point to index 0.
We also have an empty dictionary freq to keep track of the fruits inside our basket.

Step 2:

For every step, we move the right pointer r one by one and add the current fruit into the dictionary.
The dictionary will store:

• fruit type as the key

• last seen index as the value

So if the fruit repeats, we just update its index.

Step 3:

If the dictionary has more than 2 fruits → that means our basket is overloaded (we only have 2 baskets).

So now, we must remove one fruit type.

• To decide which one to remove, we check the fruit with the smallest index (because it is the oldest fruit in our window).

• Move the left pointer l just after that index.

• Remove that fruit from the dictionary.

Step 4:

At every step, we calculate the window size = r - l + 1.
Keep track of the maximum window size we ever see.

Step 5:

At the end, the maximum window size is our answer.

Here's what the code looks like

Dry Run

Start:
l = 0, res = 0, last_seen_index= {}

Step 1: r = 0 → fruit = 1

• Put into dict → last_seen_index = {1: 0}

• Dict size ≤ 2 → OK

• Window size = 0 - 0 + 1 = 1

• res = max(0,1) = 1

Step 2: r = 1 → fruit = 2

• Put into dict → last_seen_index = {1: 0, 2: 1}

• Dict size ≤ 2 → OK

• Window size = 1 - 0 + 1 = 2

• res = max(1,2) = 2

Step 3: r = 2 → fruit = 3

• Put into dict → last_seen_index = {1: 0, 2: 1, 3: 2}

• Dict size = 3 → Too many!

• Remove the fruit with smallest last index → fruit 1 (index 0)

• Move l = 0 + 1 = 1

• After removal → last_seen_index = {2: 1, 3: 2}

• Window size = 2 - 1 + 1 = 2

• res = max(2,2) = 2

Step 4: r = 3 → fruit = 2

• Update dict → last_seen_index= {2: 3, 3: 2}

• Dict size = 2 → OK

• Window size = 3 - 1 + 1 = 3

• res = max(2,3) = 3

Step 5: r = 4 → fruit = 2

• Update dict → last_seen_index = {2: 4, 3: 2}

• Dict size = 2 → OK

• Window size = 4 - 1 + 1 = 4

• res = max(3,4) = 4

Step 6: r = 5 → fruit = 3

• Update dict → last_seen_index = {2: 4, 3: 5}

• Dict size = 2 → OK

• Window size = 5 - 1 + 1 = 5

• res = max(4,5) = 5

Final Answer = 5

Why is this the optimal solution?

• We use two pointers l and r to maintain a valid window (at most 2 fruit types).

• Every fruit is added once (when r moves forward).

• Every fruit is removed once (when it l moves forward).

• So each element is processed at most 2 times → total work is proportional to n.

That’s O(n) time complexity.
Space complexity is O(2) (since the dictionary has at most 2 fruit types).

---

More to Practise (Similar Sliding Window Patterns)

1. LeetCode 3 – Longest Substring Without Repeating Characters

2. LeetCode 76 – Minimum Window Substring

3. LeetCode 340 – Longest Substring with At Most K Distinct Characters

4. LeetCode 159 – Longest Substring with At Most Two Distinct Characters

5. LeetCode 209 – Minimum Size Subarray Sum

---