Day 3: Mastering Sliding Window Beginner to Advanced

Levelling up with one of the most powerful DSA techniques

Sep 02, 2025

Mastering Sliding Window Problems: A Simple Yet Powerful Technique | by Tasmia Binte Monzoor | Medium

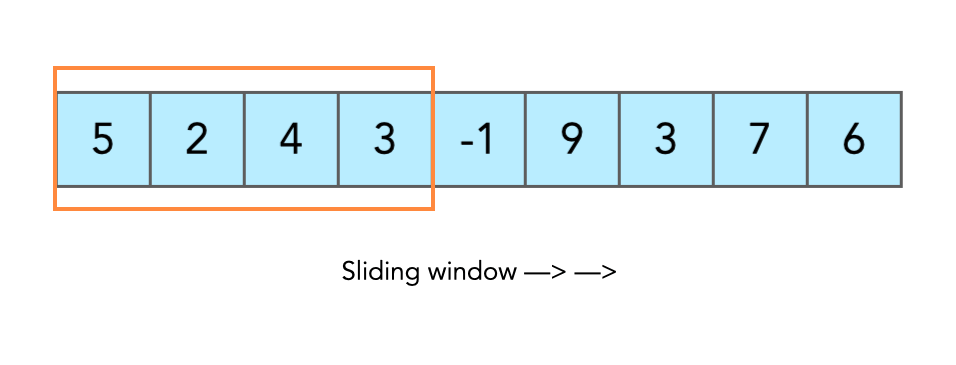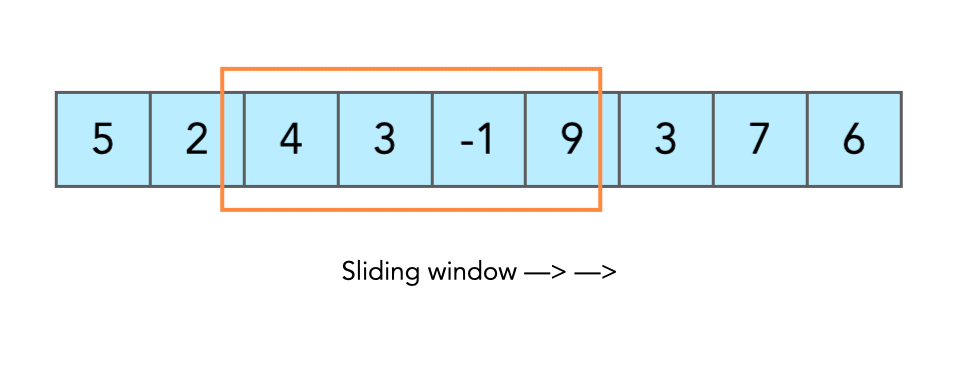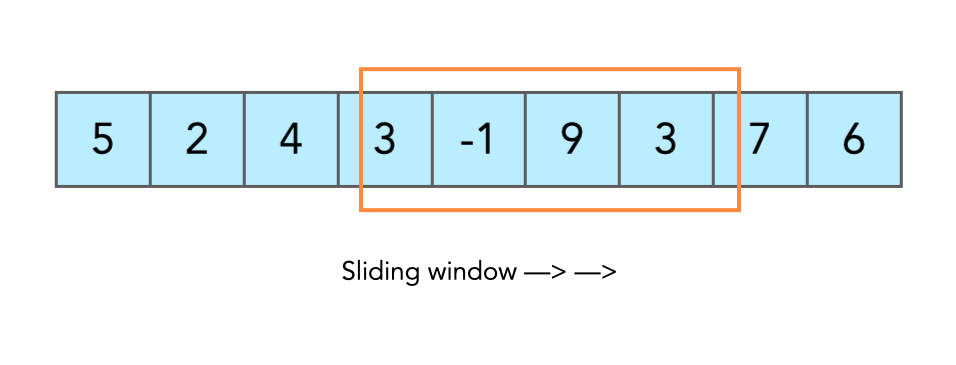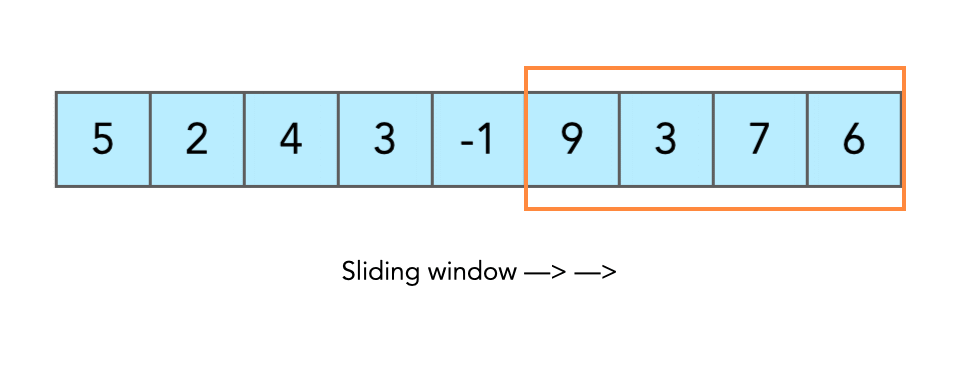
Sliding Window is a technique used to solve problems that deal with subarrays or substrings (continuous parts of an array or string).
Instead of checking every possible part one by one (which is slow), we keep a "window" that slides across the data.

Imagine you are looking outside through a window in your room.

You can only see a small portion of the street (not the whole street).
If you want to see the next part of the street, you slide the window frame to the right.
Now the view changes, but the window size stays the same.

This is exactly how Sliding Window works in programming:

Instead of checking the whole array/string again and again,
You look at a small portion (window) at a time,
And then slide it to cover the next portion.

🔑 Two Types of Sliding Window

When we talk about Sliding Window, there are mainly two patterns you’ll come across:

1. Fixed-size Window

Here, the window length is always constant.

We use two pointers: left and right.
The distance between them is always fixed = k (right-left = k).
Whenever it left moves forward by 1, right also moves forward by 1.
So the window just slides step by step, always covering exactly k the elements.

Typical use: Find max/min/average of all subarrays of size k.

2. Variable-size Window

Here, the window is not fixed. It can expand or shrink depending on conditions.

We also use two pointers: left and right.
Here, the distance is not fixed. It depends on conditions.
First, we keep moving right forward (expanding the window).
If the condition breaks (like duplicates or sum too large), we move left forward (shrinking the window).
So the window can grow or shrink dynamically until the condition is satisfied.

Typical use: Find longest/shortest subarray or substring under some rule.

Fixed-Size Sliding Window: A Meta’s Favourite Problem

Scenario:
You are a software engineer at Meta, working on Instagram Stories analytics.

Meta wants to analyse user engagement trends. You are given daily view counts for a user over n days. Your manager asks:

“Find the consecutive k days where the user was most active. Return the indices of these days.”

Input/Output Example:

views = [120, 80, 200, 150, 90, 300], k = 3
Output: [2, 3, 4]

Explanation:

Maximum sum of 3 consecutive days = 440 (200+150+90)
The days with maximum views are indices 3, 4, 5 (1-based indexing).

Solution

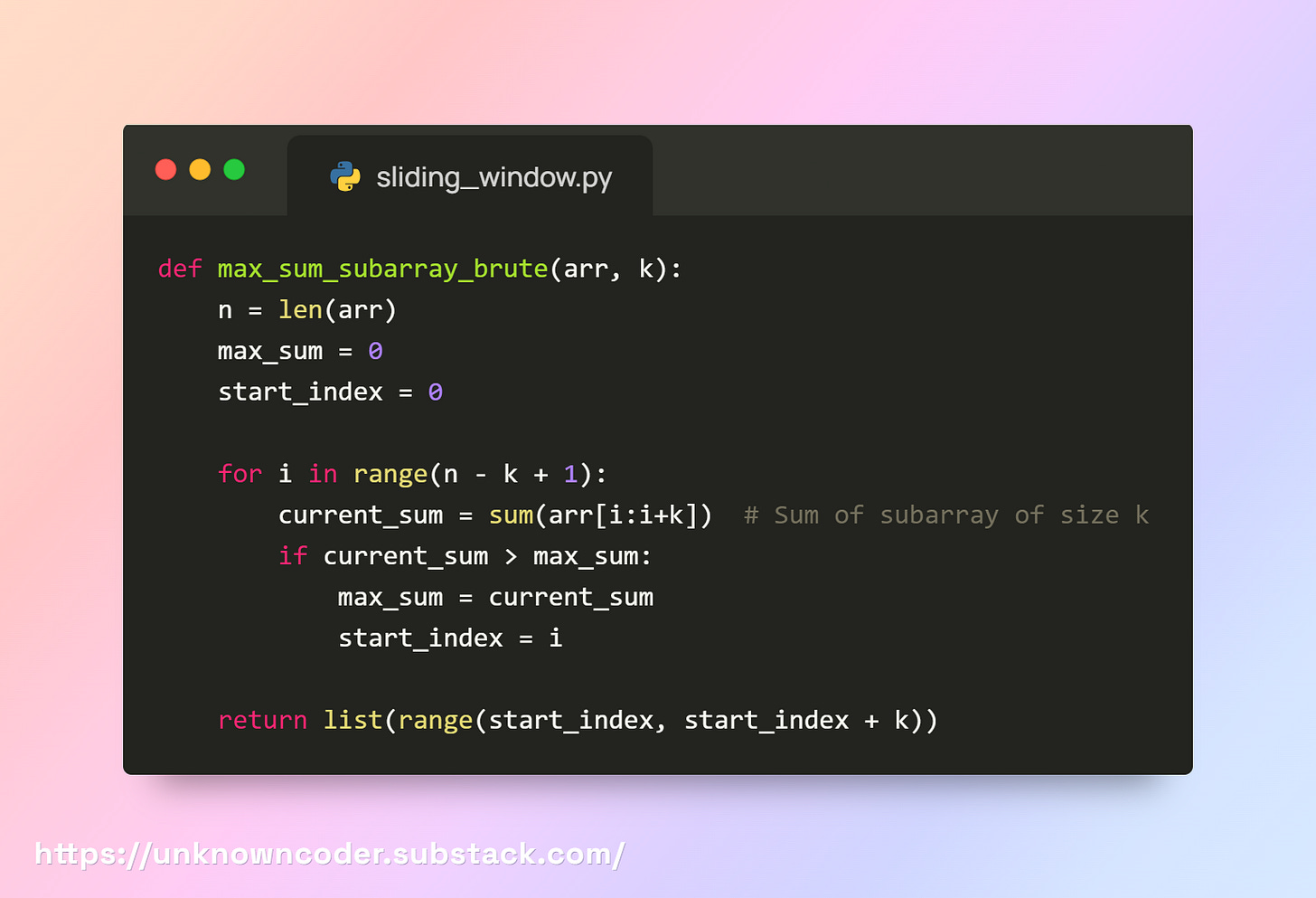
Brute Force Approach

Idea:

Check every possible subarray of size k.
Calculate the sum for each subarray.
Keep track of the maximum sum and the starting index of that subarray.

Dry Run Example

arr = [120, 80, 200, 150, 90, 300], k = 3

i = 0 → sum([120, 80, 200]) = 400 → max_sum = 400, start_index = 0
i = 1 → sum([80, 200, 150]) = 430 → max_sum = 430, start_index = 1
i = 2 → sum([200, 150, 90]) = 440 → max_sum = 440, start_index = 2
i = 3 → sum([150, 90, 300]) = 540 → max_sum = 540, start_index = 3

Output: [3, 4, 5] ✅

Time Complexity

O(n × k) → For each starting index, we sum k elements
Space Complexity: O(1) (ignoring output array)

Why this is not efficient:

For large arrays (n ~ 10⁵), recalculating the sum for every subarray is slow.
This is exactly where Sliding Window comes in to reduce it to O(n).

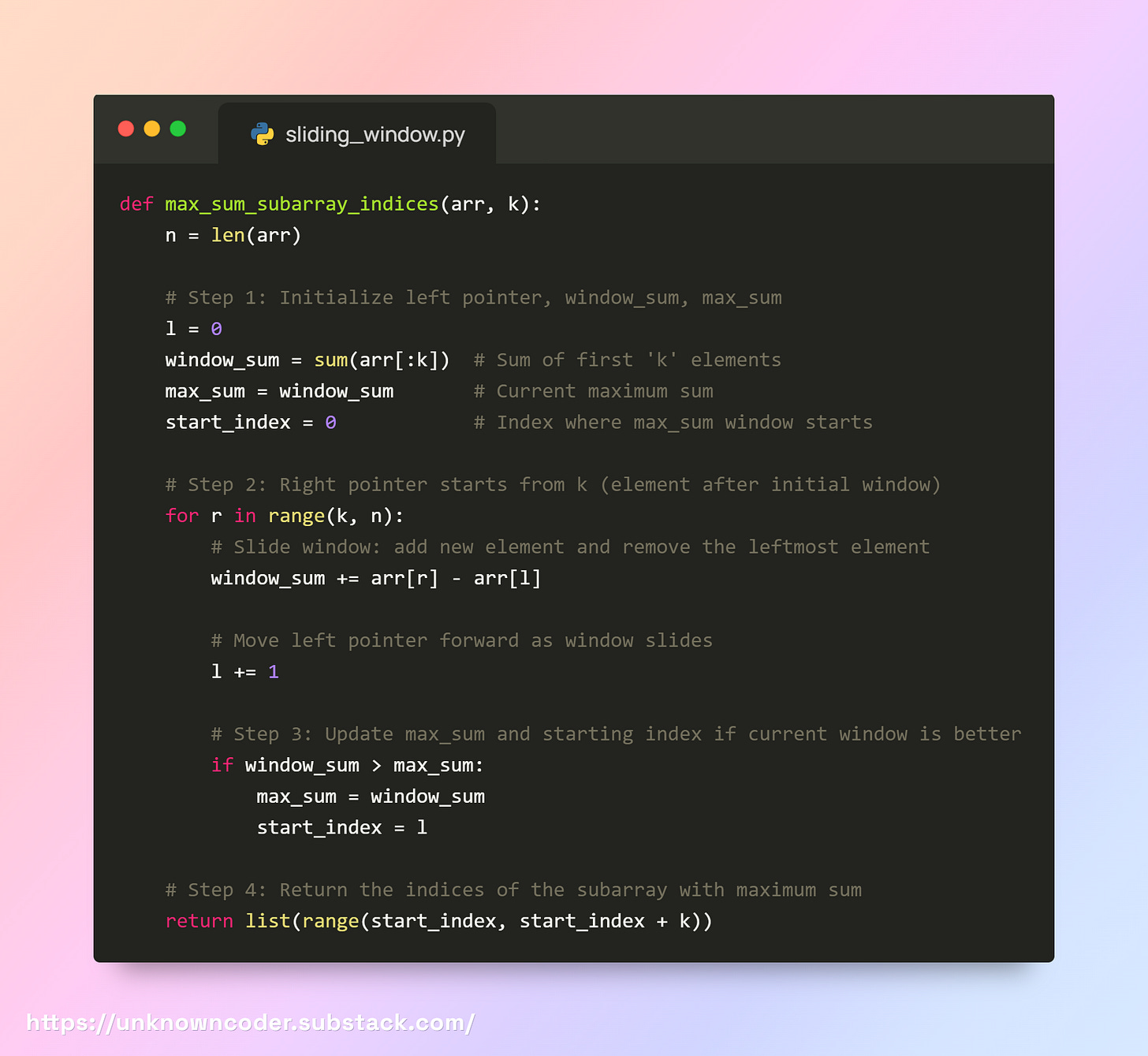
Optimal Sliding Window Code

Step-by-Step Dry Run

arr = [120, 80, 200, 150, 90, 300], k = 3

Initial window [120, 80, 200] → sum = 400 → max_sum = 400, start_index = 0
Slide window: remove 120, add 150 → [80, 200, 150] → sum = 430 → max_sum = 430, start_index = 1
Slide window: remove 80, add 90 → [200, 150, 90] → sum = 440 → max_sum = 440, start_index = 2
Slide window: remove 200, add 300 → [150, 90, 300] → sum = 540 → max_sum = 540, start_index = 3

Output: [3, 4, 5]

Complexity

Time Complexity - O(n)

Space Complexity - O(1)

Logesh

Discussion about this post