DAY 2 (Part 2): Mastering Prefix & Suffix Techniques Beginner to Advanced

In this article, we’ll dive deep into the concept of suffix sums.

Aug 28, 2025

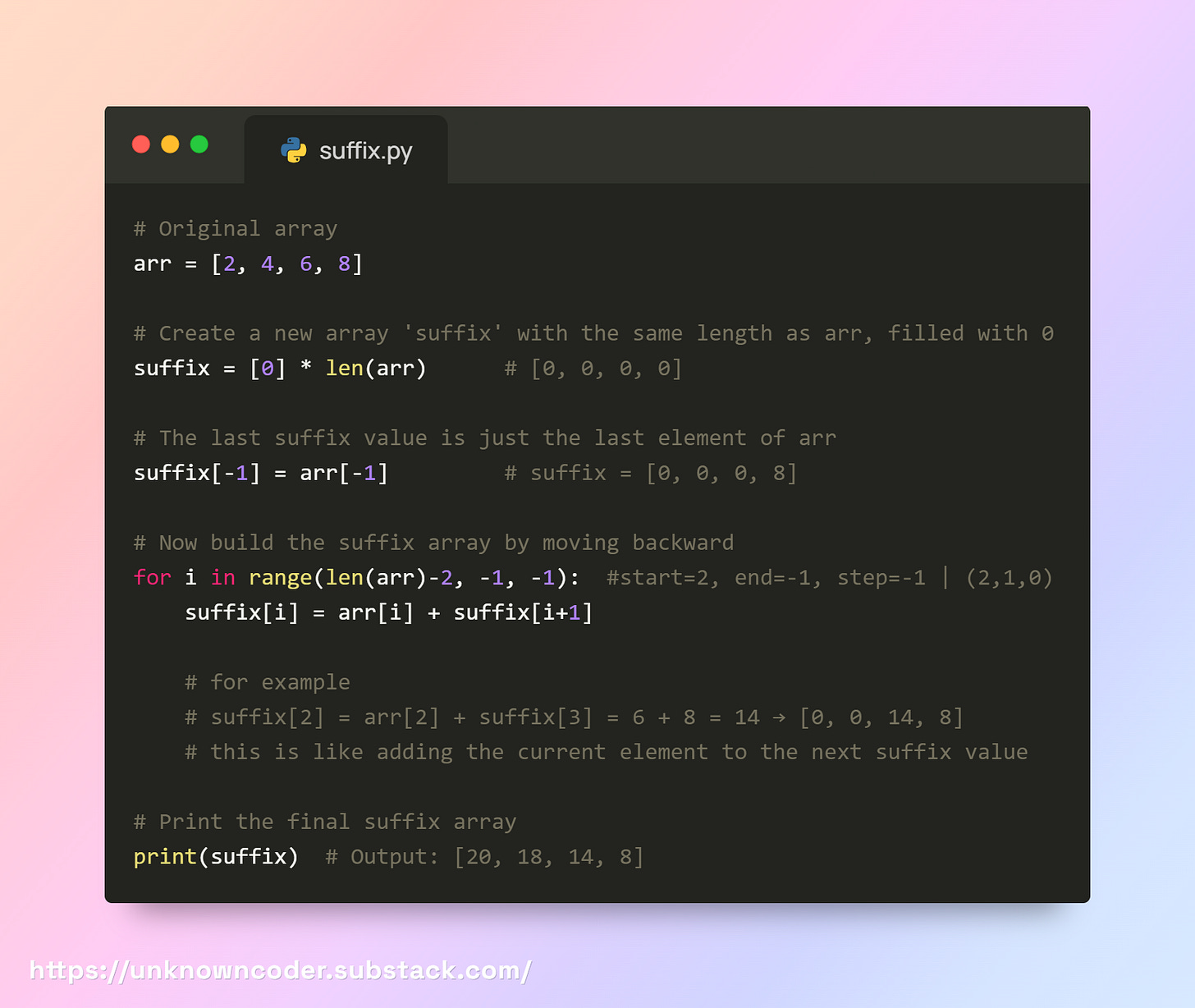
Concept of Suffix

When we talked about prefix sums, we looked at arrays from the front. Now, let’s flip the perspective. Instead of adding things up from the start, what if we begin from the end and move backward? That’s exactly what a suffix sum is.

In short:

Prefix sum → adds numbers from the beginning up to a point.
Suffix sum → adds numbers from a point to the very end.

Suffix sums are useful whenever you need to quickly calculate totals from some index to the end of an array. Instead of looping again and again, you precompute once and answer in O(1) time.

Think of the same cricket match, but this time you want to know how many runs are left after a certain over.

Instead of starting from the beginning, you look from the end of the innings and move backward. From the 20th over total, you subtract what was scored up to the 10th over, and you instantly know the runs made in the last 10 overs.

That’s the power of suffix sums: they keep track of what’s remaining, so you can answer questions looking from the back without starting over.

Working with Suffix

We know that a suffix is simply adding the next value to the previous result as we move backward in an array. But how do we actually build this in code? Let’s see.

Now someone asks:

What’s the sum from index 2 to the end (6 + 8)?
Or what’s the sum from index 1 to the end (4 + 6 + 8)?

Without a suffix, you’d add them manually each time. That’s okay for a few queries, but what if I give you 100 such questions? It quickly becomes inefficient.

With a suffix, the job becomes instant.

From index 2 to end → suffix[2] = 14
From index 1 to end → suffix[1] = 18

No repeated addition, no wasted time.

This is especially useful in problems where you’re asked about “remaining totals” from a certain position onward. Suffix sums make these queries super fast.

Let’s dive into real problem using Suffix

Amazon OA Test Question (Leetcode 560)

You are given an array representing the daily transactions of a customer’s account (positive = deposits, negative = withdrawals).

Your task is to count how many continuous periods of days have a total transaction value equal to K.

Example 1

transactions = [1,2,3,-3,1,1,1,4,2,-3], K = 3

Output = 8

Explanation:

[1, 2]
[1, 2, 3, -3]
[2, 3, -3, 1]
[3]
[3, -3, 1, 1, 1]
[-3, 1, 1, 1, 4, 2, -3]
[1, 1, 1]
[4, 2, -3]
total = 8 sub arrays

Example 2

transactions = [2, -1, 2], K = 3
Output = 1
Explanation:
Days [2, -1, 2] → total = 3

Your Turn Before Seeing the Solution

Before you look at the solution, try to solve it yourself.

Solution

Let’s first try solving this problem using the brute force approach. In brute force, we need to check all possible subarrays and calculate their sums

For example:

transactions = [1, 2, 3, -3, 1, 1, 1, 4, 2, -3], K = 3

We’ll check all subarrays one by one.

Step 1: Start from index `0`

[1] = 1 ❌
[1, 2] = 3 ✅ (count = 1)
[1, 2, 3] = 6 ❌
[1, 2, 3, -3] = 3 ✅ (count = 2)
[1, 2, 3, -3, 1] = 4 ❌
[1, 2, 3, -3, 1, 1] = 5 ❌
[1, 2, 3, -3, 1, 1, 1] = 6 ❌
[1, 2, 3, -3, 1, 1, 1, 4] = 10 ❌
… keep going

Step 2: Start from index `1`

[2] = 2 ❌
[2, 3] = 5 ❌
[2, 3, -3] = 2 ❌
[2, 3, -3, 1] = 3 ✅ (count = 3)
[2, 3, -3, 1, 1] = 4 ❌
… continue

Step 3: Start from index `2`

[3] = 3 ✅ (count = 4)
[3, -3] = 0 ❌
[3, -3, 1] = 1 ❌
[3, -3, 1, 1] = 2 ❌
[3, -3, 1, 1, 1] = 3 ✅ (count = 5)
… continue

Step 4: Start from index `3`

[-3] = -3 ❌
[-3, 1] = -2 ❌
[-3, 1, 1] = -1 ❌
[-3, 1, 1, 1] = 0 ❌
[-3, 1, 1, 1, 4] = 4 ❌
[-3, 1, 1, 1, 4, 2] = 6 ❌
[-3, 1, 1, 1, 4, 2, -3] = 3 ✅ (count = 6)

So, in the brute force method, we try every possible subarray, calculate its sum, and check if it equals K.

That means:

First fix a starting index.
Then extend the subarray by moving the ending index one step at a time.
Keep adding the values and see if the total matches K.

Since for each starting index we may scan the rest of the array, the time complexity becomes O(n²). And if we also explicitly store each subarray, it can even go up to O(n³) in terms of work.

This works for small inputs, but for large arrays (like thousands of transactions), it becomes very slow.

That’s why we need a smarter approach.

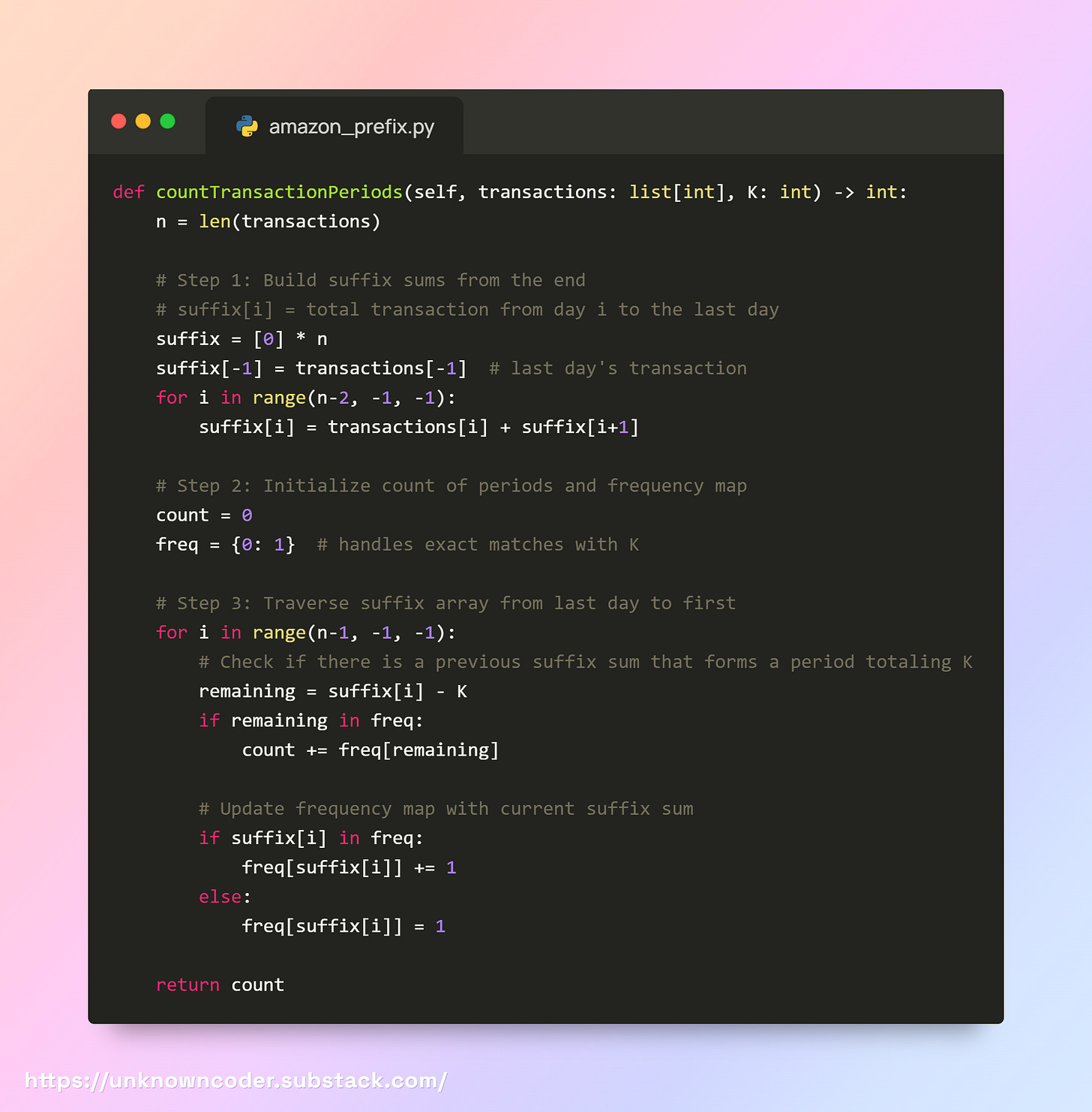
Optimal solution

For Optimal solution, we will combine the Suffix Sum concept with a Hash Map. A Hash Map is a data structure that stores values with unique keys, allowing us to quickly look up, insert, or update data. It’s perfect for keeping track of counts or frequencies while we traverse the array.

Try to understand the logic, if you can, that’s great. Otherwise, here’s the approach I’m following.

transactions = [1, 2, 3, -3, 1, 1, 1, 4, 2, -3]

then the suffix array will look like:

suffix = [9, 8, 6, 3, 6, 5, 4, 3, -1, -3]

The purpose of computing the suffix array is to precompute running totals from the back so that we can answer “remaining sum” queries (or detect subarrays equal to K) efficiently without recalculating everything.

for i in range(n-1, -1, -1):
        # Check if there is a previous suffix sum that forms a period totaling K
        remaining = suffix[i] - K
        if remaining in freq:
            count += freq[remaining]
        
        # Update frequency map with current suffix sum
        if suffix[i] in freq:
            freq[suffix[i]] += 1
        else:
            freq[suffix[i]] = 1

Now come to this part will try to dry run

Given

transactions = [1,2,3,-3,1,1,1,4,2,-3], K = 3
suffix = [9, 8, 6, 3, 6, 5, 4, 3, -1, -3]

Initialize:
freq = {0:1} (empty suffix)
count = 0

We go from right to left (index 9 → 0).
At each step: remove = suffix[i] - K.
If remove is in freq, we increase count by freq[remove].
Then we add suffix[i] into freq.

i = 9 → suffix[9] = -3

remove = -3 - 3 = -6
-6 not in map → no add.
Update freq: {0:1, -3:1}
count = 0

i = 8 → suffix[8] = -1

remove = -1 - 3 = -4
-4 not in map → no add.
Update freq: {0:1, -3:1, -1:1}
count = 0

i = 7 → suffix[7] = 3

remove = 3 - 3 = 0
0 is in map (the empty suffix).
That means from i=7 to end we already have a subarray sum = 3.
Which one? transactions[7..9] = [4,2,-3]
Increase count += 1
Update freq: {0:1, -3:1, -1:1, 3:1}
count = 1
✔ Found: [4,2,-3]

i = 6 → suffix[6] = 4

remove = 4 - 3 = 1
1 not in map → no add.
Update freq: {0:1, -3:1, -1:1, 3:1, 4:1}
count = 1

i = 5 → suffix[5] = 5

remove = 5 - 3 = 2
2 not in map → no add.
Update freq: {0:1, -3:1, -1:1, 3:1, 4:1, 5:1}
count = 1

i = 4 → suffix[4] = 6

remove = 6 - 3 = 3
3 is in map (from i=7).
Think like this: the big tail from i=4 is [1,1,1,4,2,-3] (sum = 6).
We already computed 3 previously via the tail starting at i=7, which is [4,2,-3].
So if we remove that previously-known 3 from the end, we are left with [1,1,1], which is exactly K.
Increase count += 1
Update freq: {0:1, -3:1, -1:1, 3:1, 4:1, 5:1, 6:1}
count = 2
✔ Found: [1,1,1]

i = 3 → suffix[3] = 3

remove = 3 - 3 = 0
0 is in map (empty suffix).
That means don’t remove anything from the tail [ -3,1,1,1,4,2,-3 ] — the whole tail itself sums to 3.
Increase count += 1
Update freq: {0:1, -3:1, -1:1, 3:2, 4:1, 5:1, 6:1}
count = 3
✔ Found: [-3,1,1,1,4,2,-3]

i = 2 → suffix[2] = 6

remove = 6 - 3 = 3
3 is in map with freq 2 (we have two places where suffix = 3: i=7 and i=3).
So we can remove either of those known tails to peel off a 3 from the end, giving two new subarrays:
- Remove the 3 at i=7 ([4,2,-3]) from the tail starting at i=2 ([3,-3,1,1,1,4,2,-3]) → leftover [3,-3,1,1,1].
- Remove the 3 at i=3 ([-3,1,1,1,4,2,-3]) → leftover is just [3] (the single element at i=2).
Increase count += 2
Update freq: {0:1, -3:1, -1:1, 3:2, 4:1, 5:1, 6:2}
count = 5
✔ Found: [3,-3,1,1,1], [3]

i = 1 → suffix[1] = 8

remove = 8 - 3 = 5
5 is in map (from i=5).
Big tail from i=1 is [2,3,-3,1,1,1,4,2,-3] (sum = 8).
We already have a suffix 5 starting at i=5 → that tail is [1,1,1,4,2,-3].
Remove that known tail (sum 5) → leftover [2,3,-3,1] = 3.
Increase count += 1
Update freq: {0:1, -3:1, -1:1, 3:2, 4:1, 5:1, 6:2, 8:1}
count = 6
✔ Found: [2,3,-3,1]

i = 0 → suffix[0] = 9

remove = 9 - 3 = 6
6 is in map with freq 2 (we’ve seen suffix 6 at i=4 and i=2).
So we can remove either:
- Remove 6 at i=4 ([1,1,1,4,2,-3]) → leftover [1,2,3,-3] = 3.
- Remove 6 at i=2 ([3,-3,1,1,1,4,2,-3]) → leftover [1,2] = 3.
Increase count += 2
Update freq: {0:1, -3:1, -1:1, 3:2, 4:1, 5:1, 6:2, 8:1, 9:1}
count = 8
✔ Found: [1,2,3,-3], [1,2]

Final `count = 8` ✅

All subarrays we found (in any order):

[4,2,-3]
[1,1,1]
[-3,1,1,1,4,2,-3]
[3,-3,1,1,1]
[3]
[2,3,-3,1]
[1,2,3,-3]
[1,2]

This keeps the remove → leftover reasoning at every step and adds the count correctly to reach 8.

So, this is how we can solve the problem in O(N) time. You can also try solving it using the prefix approach as well.

If you’d like to practice more with the same idea, here are 5 problems that follow a similar pattern:

Logesh

Discussion about this post