DAY 2: Mastering Prefix & Suffix Techniques Beginner to Advanced

Precompute smartly, answer instantly: a complete guide to prefix & suffix techniques.

Prefix and suffix techniques are among the simplest yet most powerful tools in problem-solving. They allow us to precompute useful information and answer queries in constant time instead of recalculating repeatedly. From basic range sums to advanced interview problems like Trapping Rain Water or KMP string matching, these techniques form the backbone of efficient solutions.

In this article, I’ll first walk you through the basics of prefix and suffix techniques, and then we’ll solve problems at three levels like beginner, intermediate, and advanced, to see how these concepts apply in real coding challenges.

Concept of Prefix

A prefix is simply the cumulative information we collect from the start of a sequence up to a certain point. Instead of recalculating from the beginning each time, we build a prefix array that stores these partial results.

Once this prefix array is built, any query about the sequence can be answered quickly, because the work has already been done step by step.

Think of a cricket scoreboard. After every over, the scoreboard shows the total runs so far.

• If you want to know something about runs between the 6th and 15th overs, you don’t need to count them all again.

• You can just look at the scoreboard at over 15 and compare it with the scoreboard at over 5.

That’s the power of prefixes: they keep track of progress as you move forward, so you can answer questions without starting over.

---

Working with Prefix

We know that a prefix is simply adding the previous value to the next value as we move forward in an array. But how do we actually implement this in code? Let’s see.

Now that we know how to build the prefix array, the big question is: what’s the use of it?

Normally, if you want the sum of elements between two indices in an array, you would loop through all those elements and add them up. That takes O(n) time for every query.

With the prefix array, you don’t need to add again. The work is already done. You just subtract two values and get the answer in O(1) time.

Imagine this:

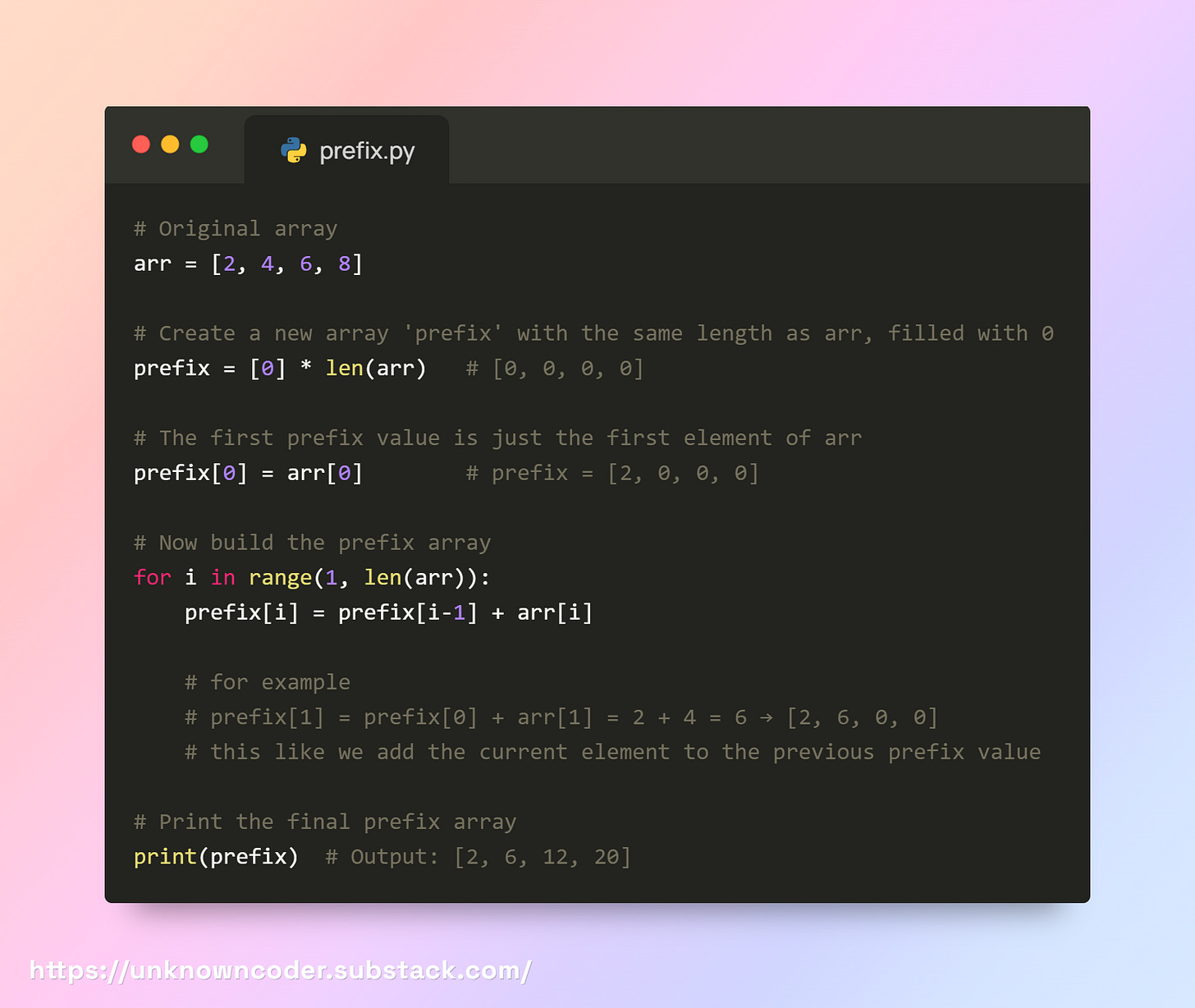
arr = [2, 4, 6, 8]
prefix = [2, 6, 12, 20]

Someone asks:

• What’s the sum from index 1 to 3 (4 + 6 + 8)?

• Or what’s the sum from index 2 to 3 (6 + 8)?

If you didn’t have prefix, you’d add them one by one every time. That’s fine for one or two queries, but what if I give you 100 such questions? It quickly gets messy.

With prefix, the job becomes instant.
You just do:

sum(l to r) = prfix[r] - prefix[l-1]

• For index 1 to 3 → prefix[3] - prefix[0] = 20 - 2 = 18

• For index 2 to 3 → prefix[3] - prefix[1] = 20 - 6 = 14

No repeated addition, no wasted time.

This is called a Range Query when you’re asked to find the sum of numbers between two positions in an array. Prefix sums make these queries super fast.

---

Let’s dive into real problem using Prefix

Google Level-1 Problem:

You have an array of integers. Find an index where the sum of elements to the left is equal to the sum of elements to the right. If multiple indices exist, return the first one. If none, return -1.

Suppose we have an array:

arr = [1, 7, 3, 6, 5, 6]

We want to find an index i such that:

sum of elements to the left of i == sum of elements to the right of i

Here how its work..

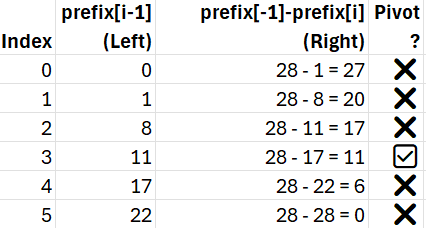
Index 0: arr[0] = 1

• Left sum = 0 (no elements to the left of 0th index)

• Right sum = 7 + 3 + 6 + 5 + 6 = 27

• ❌ Not equal → index 0 is not pivot

Index 1: arr[1] = 7

• Left sum = 1

• Right sum = 3 + 6 + 5 + 6 = 20

• ❌ Not equal → index 1 is not pivot

Index 2: arr[2] = 3

• Left sum = 1 + 7 = 8

• Right sum = 6 + 5 + 6 = 17

• ❌ Not equal → index 2 is not pivot

Index 3: arr[3] = 6

• Left sum = 1 + 7 + 3 = 11

• Right sum = 5 + 6 = 11

• ✅ Equal → pivot found!

Index 4: arr[4] = 5

• Left sum = 1 + 7 + 3 + 6 = 17

• Right sum = 6

• ❌ Not equal → index 4 is not pivot

Index 5: arr[5] = 6

• Left sum = 1 + 7 + 3 + 6 + 5 = 22

• Right sum = 0

• ❌ Not equal → index 5 is not pivot

So the answer is 3; at the 3rd index, left == right.

---

Your Turn Before Seeing the Solution

Before you look at the solution, try to solve it yourself.

I know there are many ways to approach this problem brute force, prefix sums, running totals…

Challenge yourself and see if you can find the pivot index in your own way.

---

Solution

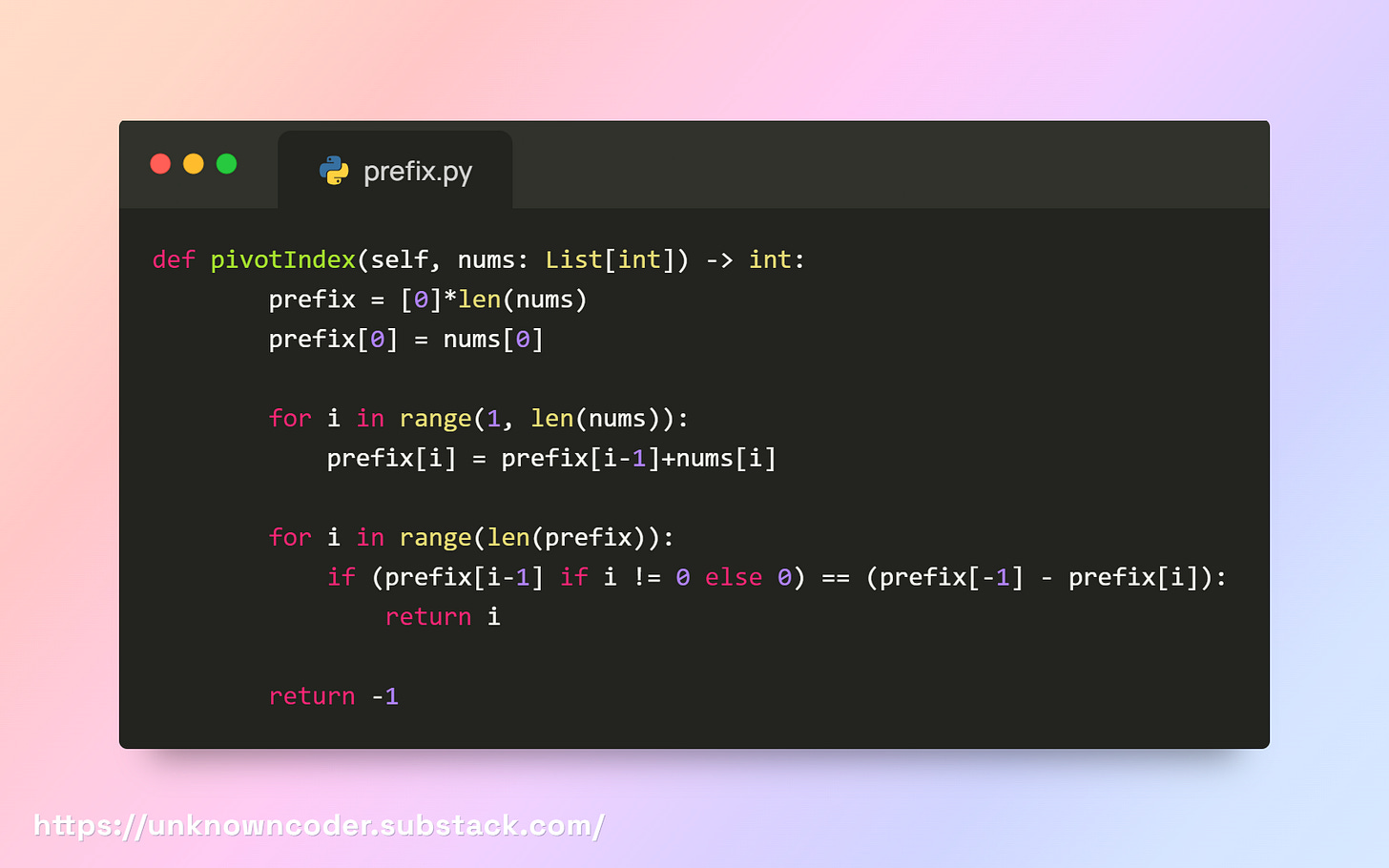
Step 1: Create prefix sum array

prefix = [0]*len(nums)
prefix[0] = nums[0]

for i in range(1, len(nums)):
    prefix[i] = prefix[i-1] + nums[i]

• prefix[i] stores the sum of all numbers from index 0 to i

• Example:

nums = [1, 7, 3, 6, 5, 6]
prefix = [1, 8, 11, 17, 22, 28]

Step 2: Loop through all indices to find pivot

for i in range(len(prefix)):
    if (prefix[i-1] if i != 0 else 0) == (prefix[-1] - prefix[i]):
        return i

• Left sum: prefix[i-1] → sum of elements before index i

  • For index 0, there’s nothing on the left → 0

• Right sum: prefix[-1] - prefix[i] → total sum minus sum up to index i

• ✅ If left sum equals right sum → i is the pivot

Step 3: No pivot found

return -1

• If no index balances the left and right sums, return -1.

Step 4: Complexity

• Time: O(n) → prefix sum array + single loop

• Space: O(n) → prefix sum array

Step 5: Intuition

• Think of prefix[i-1] as everything to the left

• Think of prefix[-1] - prefix[i] as everything to the right

• If they are equal → pivot found

Your turn (similar problem from LeetCode):

1991. Find the Middle Index in Array

1013. Partition Array Into Three Parts With Equal Sum

2574. Left and Right Sum Differences

2270. Number of Ways to Split Array

2256. Minimum Average Difference

---

How to identify?

Certain keywords or problem descriptions signal that the Prefix Sum pattern might be the right approach. Look out for the following clues:

1. Range-based Queries

• Keywords: Range sum, subarray sum, interval sum, between indices

• Problems asking to calculate the sum of elements between two indices repeatedly.
  Example: “Find the sum of elements from the index i to j efficiently.”

2. Cumulative or Running Total

• Keywords: Cumulative, running sum, progressive sum, prefix, suffix

• Tasks involving precomputing totals for efficiency or comparisons.
  Example: “Find the total number of items sold between day x and y.”

3. Subarray Sum Properties

• Keywords: Subarray with a given sum, count of subarrays, sum divisible by k

• Problems involving counting or finding subarrays based on their sum.
  Example: “Count the number of subarrays where the sum is equal to k.”

4. Equilibrium Points

• Keywords: Balanced sum, left equals right, split point, equilibrium index

• Finding indices where the sum of elements on the left equals the sum on the right.
  Example: “Find an index i where the sum of elements to the left equals the sum to the right.”

5. Modular Arithmetic with Sums

• Keywords: Divisible by k, remainder, modulus

• Tasks involving sums that meet modular conditions.
  Example: “Find all subarrays whose sum is divisible by k.”

6. Difference of Sums

• Keywords: Difference in range, change in total, net sum between ranges

• Situations where subtracting one cumulative value from another simplifies computation.
  Example: “Find the difference in sales between two periods.”

---